Closure to be used in sim_distribution(). The form is based on the bi-Gaussian
function described in doi:10.1186/1471-2105-11-559
.
sim_parabola(
alpha = 0,
mu = 200,
sigma = 70,
sigma_right = NULL,
log_space = FALSE,
plot = FALSE
)Arguments
- alpha, mu, sigma
Parameters that control the shape of the parabola. Can be a single value or a vector of the same length as the number of ages in the simulation (e.g., allowing age-specific depth associations).
- sigma_right
Optional parameter to impose asymmetry by specifying a different
sigmafor the right side. If used,sigmadefines the width of the left side. Ignored ifNULL.- log_space
Logical. Should the shape of the parabola be defined in log space? If
TRUE, parameters are assumed to be logged, and inputxvalues are log-transformed. This produces a lognormal-like curve with a heavier right tail and forces low values near zero.- plot
Logical. Should a simple plot of the simulated values be produced?
Value
A function that can be passed to sim_distribution().
Examples
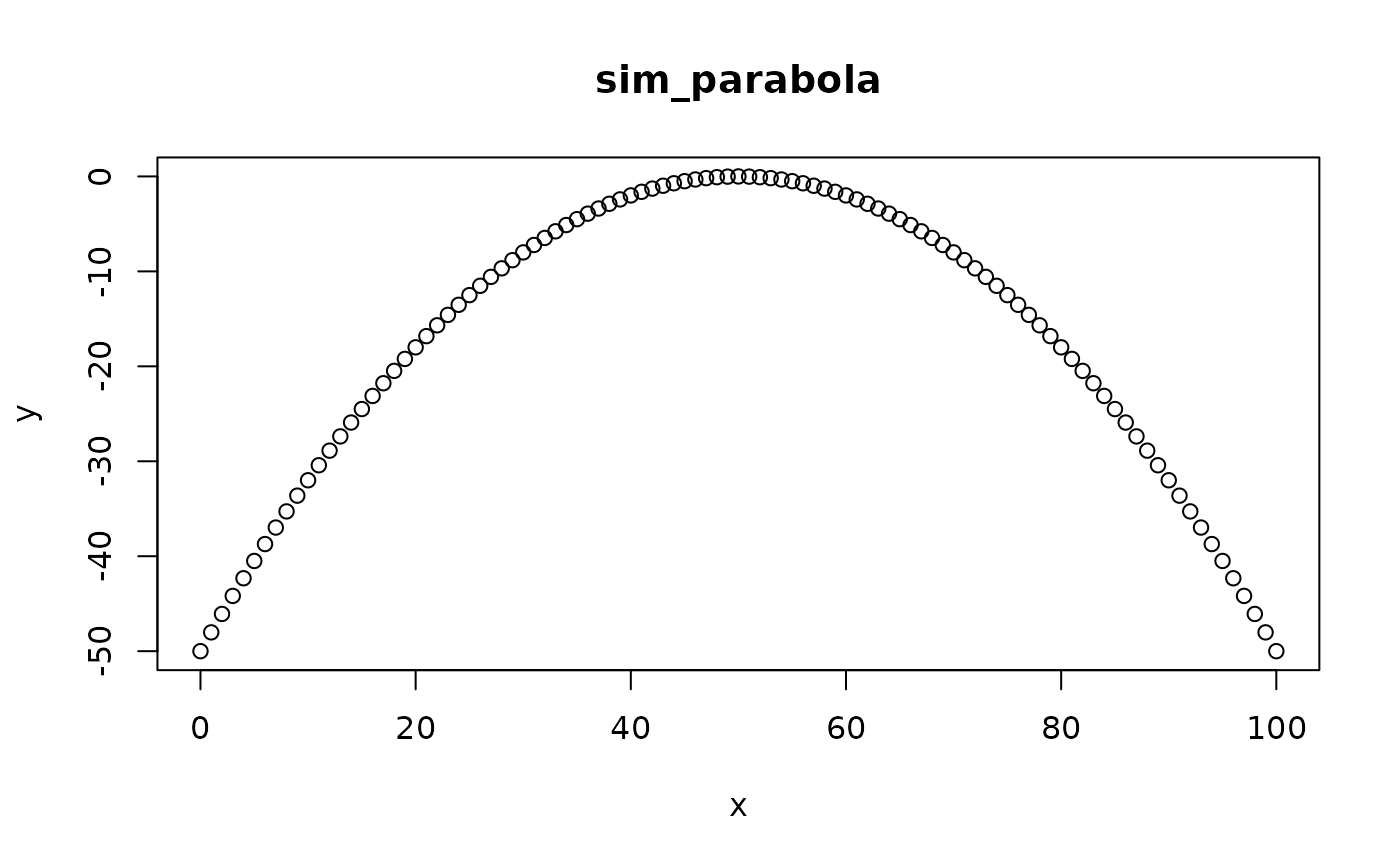
parabola_fun <- sim_parabola(mu = 50, sigma = 5, plot = TRUE)
parabola_fun(data.frame(depth = 0:100))
 #> [1] -50.00 -48.02 -46.08 -44.18 -42.32 -40.50 -38.72 -36.98 -35.28 -33.62
#> [11] -32.00 -30.42 -28.88 -27.38 -25.92 -24.50 -23.12 -21.78 -20.48 -19.22
#> [21] -18.00 -16.82 -15.68 -14.58 -13.52 -12.50 -11.52 -10.58 -9.68 -8.82
#> [31] -8.00 -7.22 -6.48 -5.78 -5.12 -4.50 -3.92 -3.38 -2.88 -2.42
#> [41] -2.00 -1.62 -1.28 -0.98 -0.72 -0.50 -0.32 -0.18 -0.08 -0.02
#> [51] 0.00 -0.02 -0.08 -0.18 -0.32 -0.50 -0.72 -0.98 -1.28 -1.62
#> [61] -2.00 -2.42 -2.88 -3.38 -3.92 -4.50 -5.12 -5.78 -6.48 -7.22
#> [71] -8.00 -8.82 -9.68 -10.58 -11.52 -12.50 -13.52 -14.58 -15.68 -16.82
#> [81] -18.00 -19.22 -20.48 -21.78 -23.12 -24.50 -25.92 -27.38 -28.88 -30.42
#> [91] -32.00 -33.62 -35.28 -36.98 -38.72 -40.50 -42.32 -44.18 -46.08 -48.02
#> [101] -50.00
parabola_fun <- sim_parabola(mu = log(40), sigma = 0.5, log_space = FALSE, plot = TRUE)
parabola_fun(data.frame(depth = 0:100))
#> [1] -50.00 -48.02 -46.08 -44.18 -42.32 -40.50 -38.72 -36.98 -35.28 -33.62
#> [11] -32.00 -30.42 -28.88 -27.38 -25.92 -24.50 -23.12 -21.78 -20.48 -19.22
#> [21] -18.00 -16.82 -15.68 -14.58 -13.52 -12.50 -11.52 -10.58 -9.68 -8.82
#> [31] -8.00 -7.22 -6.48 -5.78 -5.12 -4.50 -3.92 -3.38 -2.88 -2.42
#> [41] -2.00 -1.62 -1.28 -0.98 -0.72 -0.50 -0.32 -0.18 -0.08 -0.02
#> [51] 0.00 -0.02 -0.08 -0.18 -0.32 -0.50 -0.72 -0.98 -1.28 -1.62
#> [61] -2.00 -2.42 -2.88 -3.38 -3.92 -4.50 -5.12 -5.78 -6.48 -7.22
#> [71] -8.00 -8.82 -9.68 -10.58 -11.52 -12.50 -13.52 -14.58 -15.68 -16.82
#> [81] -18.00 -19.22 -20.48 -21.78 -23.12 -24.50 -25.92 -27.38 -28.88 -30.42
#> [91] -32.00 -33.62 -35.28 -36.98 -38.72 -40.50 -42.32 -44.18 -46.08 -48.02
#> [101] -50.00
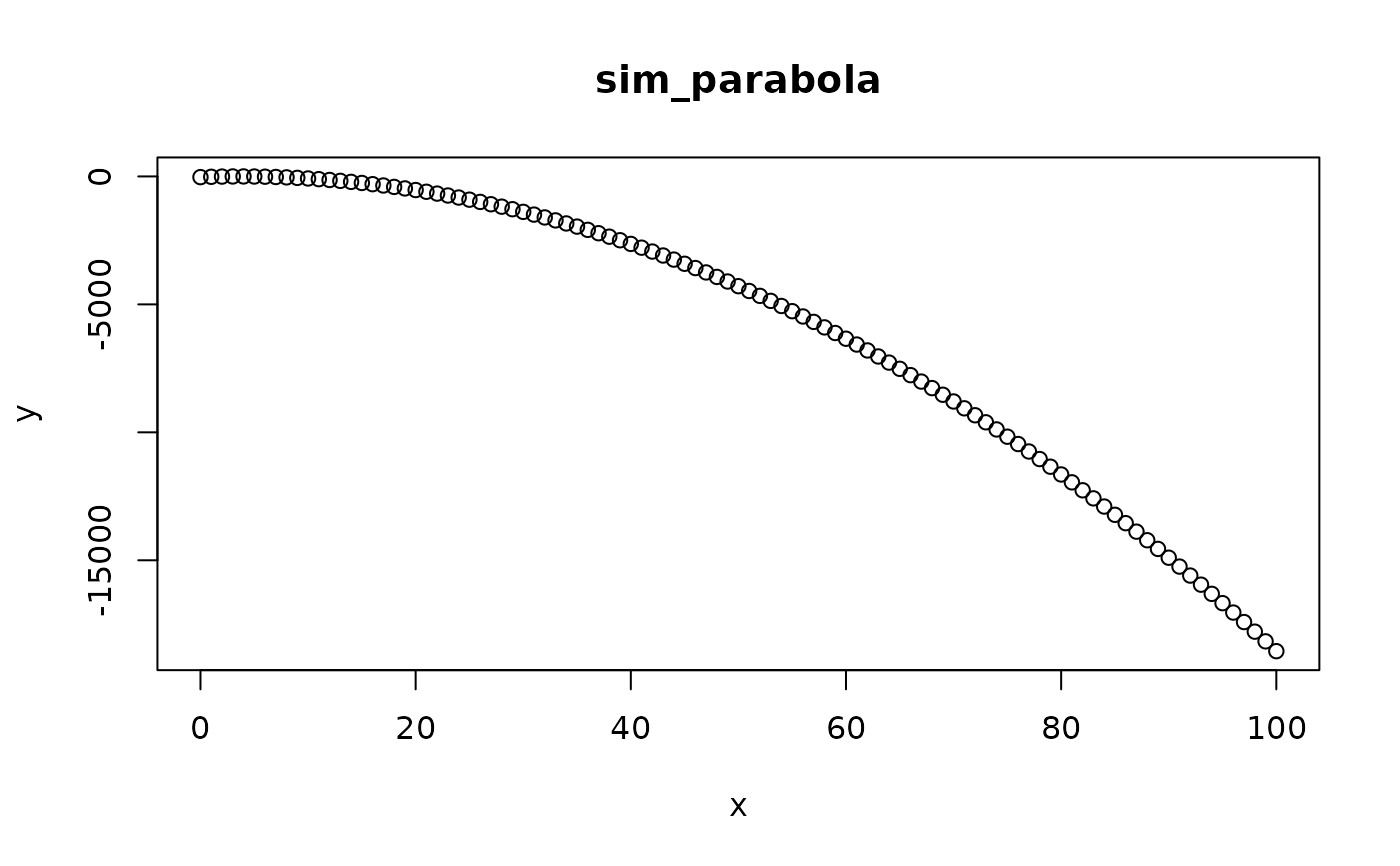
parabola_fun <- sim_parabola(mu = log(40), sigma = 0.5, log_space = FALSE, plot = TRUE)
parabola_fun(data.frame(depth = 0:100))
 #> [1] -2.721566e+01 -1.446015e+01 -5.704628e+00 -9.491098e-01 -1.935920e-01
#> [6] -3.438074e+00 -1.068256e+01 -2.192704e+01 -3.717152e+01 -5.641600e+01
#> [11] -7.966049e+01 -1.069050e+02 -1.381494e+02 -1.733939e+02 -2.126384e+02
#> [16] -2.558829e+02 -3.031274e+02 -3.543719e+02 -4.096163e+02 -4.688608e+02
#> [21] -5.321053e+02 -5.993498e+02 -6.705943e+02 -7.458388e+02 -8.250832e+02
#> [26] -9.083277e+02 -9.955722e+02 -1.086817e+03 -1.182061e+03 -1.281306e+03
#> [31] -1.384550e+03 -1.491795e+03 -1.603039e+03 -1.718284e+03 -1.837528e+03
#> [36] -1.960773e+03 -2.088017e+03 -2.219262e+03 -2.354506e+03 -2.493750e+03
#> [41] -2.636995e+03 -2.784239e+03 -2.935484e+03 -3.090728e+03 -3.249973e+03
#> [46] -3.413217e+03 -3.580462e+03 -3.751706e+03 -3.926951e+03 -4.106195e+03
#> [51] -4.289440e+03 -4.476684e+03 -4.667929e+03 -4.863173e+03 -5.062418e+03
#> [56] -5.265662e+03 -5.472907e+03 -5.684151e+03 -5.899396e+03 -6.118640e+03
#> [61] -6.341885e+03 -6.569129e+03 -6.800374e+03 -7.035618e+03 -7.274863e+03
#> [66] -7.518107e+03 -7.765351e+03 -8.016596e+03 -8.271840e+03 -8.531085e+03
#> [71] -8.794329e+03 -9.061574e+03 -9.332818e+03 -9.608063e+03 -9.887307e+03
#> [76] -1.017055e+04 -1.045780e+04 -1.074904e+04 -1.104429e+04 -1.134353e+04
#> [81] -1.164677e+04 -1.195402e+04 -1.226526e+04 -1.258051e+04 -1.289975e+04
#> [86] -1.322300e+04 -1.355024e+04 -1.388149e+04 -1.421673e+04 -1.455597e+04
#> [91] -1.489922e+04 -1.524646e+04 -1.559771e+04 -1.595295e+04 -1.631220e+04
#> [96] -1.667544e+04 -1.704269e+04 -1.741393e+04 -1.778917e+04 -1.816842e+04
#> [101] -1.855166e+04
parabola_fun <- sim_parabola(mu = c(50, 120), sigma = c(5, 3), plot = TRUE)
parabola_fun(expand.grid(depth = 1:200, age = 1:2))
#> [1] -2.721566e+01 -1.446015e+01 -5.704628e+00 -9.491098e-01 -1.935920e-01
#> [6] -3.438074e+00 -1.068256e+01 -2.192704e+01 -3.717152e+01 -5.641600e+01
#> [11] -7.966049e+01 -1.069050e+02 -1.381494e+02 -1.733939e+02 -2.126384e+02
#> [16] -2.558829e+02 -3.031274e+02 -3.543719e+02 -4.096163e+02 -4.688608e+02
#> [21] -5.321053e+02 -5.993498e+02 -6.705943e+02 -7.458388e+02 -8.250832e+02
#> [26] -9.083277e+02 -9.955722e+02 -1.086817e+03 -1.182061e+03 -1.281306e+03
#> [31] -1.384550e+03 -1.491795e+03 -1.603039e+03 -1.718284e+03 -1.837528e+03
#> [36] -1.960773e+03 -2.088017e+03 -2.219262e+03 -2.354506e+03 -2.493750e+03
#> [41] -2.636995e+03 -2.784239e+03 -2.935484e+03 -3.090728e+03 -3.249973e+03
#> [46] -3.413217e+03 -3.580462e+03 -3.751706e+03 -3.926951e+03 -4.106195e+03
#> [51] -4.289440e+03 -4.476684e+03 -4.667929e+03 -4.863173e+03 -5.062418e+03
#> [56] -5.265662e+03 -5.472907e+03 -5.684151e+03 -5.899396e+03 -6.118640e+03
#> [61] -6.341885e+03 -6.569129e+03 -6.800374e+03 -7.035618e+03 -7.274863e+03
#> [66] -7.518107e+03 -7.765351e+03 -8.016596e+03 -8.271840e+03 -8.531085e+03
#> [71] -8.794329e+03 -9.061574e+03 -9.332818e+03 -9.608063e+03 -9.887307e+03
#> [76] -1.017055e+04 -1.045780e+04 -1.074904e+04 -1.104429e+04 -1.134353e+04
#> [81] -1.164677e+04 -1.195402e+04 -1.226526e+04 -1.258051e+04 -1.289975e+04
#> [86] -1.322300e+04 -1.355024e+04 -1.388149e+04 -1.421673e+04 -1.455597e+04
#> [91] -1.489922e+04 -1.524646e+04 -1.559771e+04 -1.595295e+04 -1.631220e+04
#> [96] -1.667544e+04 -1.704269e+04 -1.741393e+04 -1.778917e+04 -1.816842e+04
#> [101] -1.855166e+04
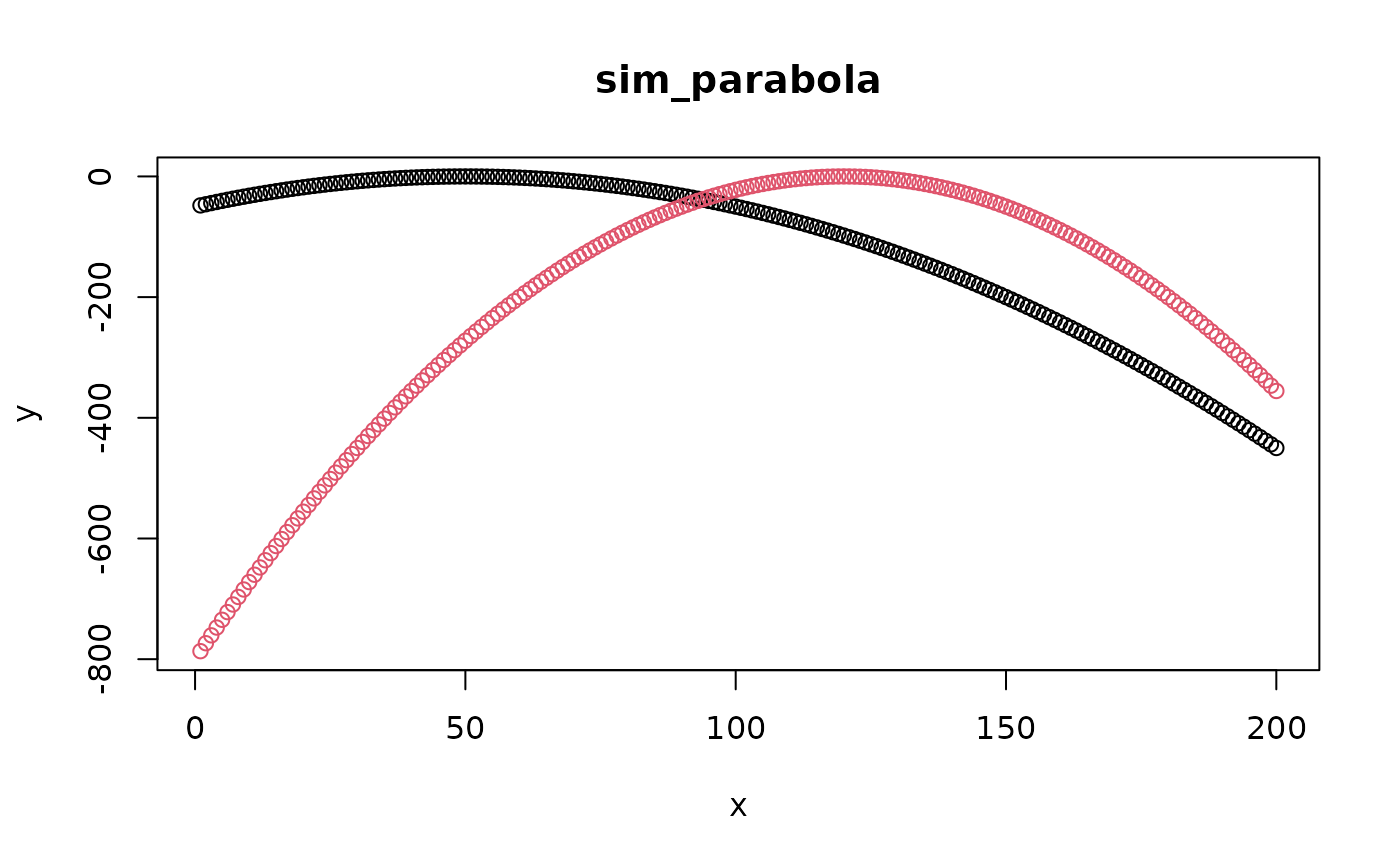
parabola_fun <- sim_parabola(mu = c(50, 120), sigma = c(5, 3), plot = TRUE)
parabola_fun(expand.grid(depth = 1:200, age = 1:2))
 #> [1] -48.02000000 -46.08000000 -44.18000000 -42.32000000 -40.50000000
#> [6] -38.72000000 -36.98000000 -35.28000000 -33.62000000 -32.00000000
#> [11] -30.42000000 -28.88000000 -27.38000000 -25.92000000 -24.50000000
#> [16] -23.12000000 -21.78000000 -20.48000000 -19.22000000 -18.00000000
#> [21] -16.82000000 -15.68000000 -14.58000000 -13.52000000 -12.50000000
#> [26] -11.52000000 -10.58000000 -9.68000000 -8.82000000 -8.00000000
#> [31] -7.22000000 -6.48000000 -5.78000000 -5.12000000 -4.50000000
#> [36] -3.92000000 -3.38000000 -2.88000000 -2.42000000 -2.00000000
#> [41] -1.62000000 -1.28000000 -0.98000000 -0.72000000 -0.50000000
#> [46] -0.32000000 -0.18000000 -0.08000000 -0.02000000 0.00000000
#> [51] -0.02000000 -0.08000000 -0.18000000 -0.32000000 -0.50000000
#> [56] -0.72000000 -0.98000000 -1.28000000 -1.62000000 -2.00000000
#> [61] -2.42000000 -2.88000000 -3.38000000 -3.92000000 -4.50000000
#> [66] -5.12000000 -5.78000000 -6.48000000 -7.22000000 -8.00000000
#> [71] -8.82000000 -9.68000000 -10.58000000 -11.52000000 -12.50000000
#> [76] -13.52000000 -14.58000000 -15.68000000 -16.82000000 -18.00000000
#> [81] -19.22000000 -20.48000000 -21.78000000 -23.12000000 -24.50000000
#> [86] -25.92000000 -27.38000000 -28.88000000 -30.42000000 -32.00000000
#> [91] -33.62000000 -35.28000000 -36.98000000 -38.72000000 -40.50000000
#> [96] -42.32000000 -44.18000000 -46.08000000 -48.02000000 -50.00000000
#> [101] -52.02000000 -54.08000000 -56.18000000 -58.32000000 -60.50000000
#> [106] -62.72000000 -64.98000000 -67.28000000 -69.62000000 -72.00000000
#> [111] -74.42000000 -76.88000000 -79.38000000 -81.92000000 -84.50000000
#> [116] -87.12000000 -89.78000000 -92.48000000 -95.22000000 -98.00000000
#> [121] -100.82000000 -103.68000000 -106.58000000 -109.52000000 -112.50000000
#> [126] -115.52000000 -118.58000000 -121.68000000 -124.82000000 -128.00000000
#> [131] -131.22000000 -134.48000000 -137.78000000 -141.12000000 -144.50000000
#> [136] -147.92000000 -151.38000000 -154.88000000 -158.42000000 -162.00000000
#> [141] -165.62000000 -169.28000000 -172.98000000 -176.72000000 -180.50000000
#> [146] -184.32000000 -188.18000000 -192.08000000 -196.02000000 -200.00000000
#> [151] -204.02000000 -208.08000000 -212.18000000 -216.32000000 -220.50000000
#> [156] -224.72000000 -228.98000000 -233.28000000 -237.62000000 -242.00000000
#> [161] -246.42000000 -250.88000000 -255.38000000 -259.92000000 -264.50000000
#> [166] -269.12000000 -273.78000000 -278.48000000 -283.22000000 -288.00000000
#> [171] -292.82000000 -297.68000000 -302.58000000 -307.52000000 -312.50000000
#> [176] -317.52000000 -322.58000000 -327.68000000 -332.82000000 -338.00000000
#> [181] -343.22000000 -348.48000000 -353.78000000 -359.12000000 -364.50000000
#> [186] -369.92000000 -375.38000000 -380.88000000 -386.42000000 -392.00000000
#> [191] -397.62000000 -403.28000000 -408.98000000 -414.72000000 -420.50000000
#> [196] -426.32000000 -432.18000000 -438.08000000 -444.02000000 -450.00000000
#> [201] -786.72222222 -773.55555556 -760.50000000 -747.55555556 -734.72222222
#> [206] -722.00000000 -709.38888889 -696.88888889 -684.50000000 -672.22222222
#> [211] -660.05555556 -648.00000000 -636.05555556 -624.22222222 -612.50000000
#> [216] -600.88888889 -589.38888889 -578.00000000 -566.72222222 -555.55555556
#> [221] -544.50000000 -533.55555556 -522.72222222 -512.00000000 -501.38888889
#> [226] -490.88888889 -480.50000000 -470.22222222 -460.05555556 -450.00000000
#> [231] -440.05555556 -430.22222222 -420.50000000 -410.88888889 -401.38888889
#> [236] -392.00000000 -382.72222222 -373.55555556 -364.50000000 -355.55555556
#> [241] -346.72222222 -338.00000000 -329.38888889 -320.88888889 -312.50000000
#> [246] -304.22222222 -296.05555556 -288.00000000 -280.05555556 -272.22222222
#> [251] -264.50000000 -256.88888889 -249.38888889 -242.00000000 -234.72222222
#> [256] -227.55555556 -220.50000000 -213.55555556 -206.72222222 -200.00000000
#> [261] -193.38888889 -186.88888889 -180.50000000 -174.22222222 -168.05555556
#> [266] -162.00000000 -156.05555556 -150.22222222 -144.50000000 -138.88888889
#> [271] -133.38888889 -128.00000000 -122.72222222 -117.55555556 -112.50000000
#> [276] -107.55555556 -102.72222222 -98.00000000 -93.38888889 -88.88888889
#> [281] -84.50000000 -80.22222222 -76.05555556 -72.00000000 -68.05555556
#> [286] -64.22222222 -60.50000000 -56.88888889 -53.38888889 -50.00000000
#> [291] -46.72222222 -43.55555556 -40.50000000 -37.55555556 -34.72222222
#> [296] -32.00000000 -29.38888889 -26.88888889 -24.50000000 -22.22222222
#> [301] -20.05555556 -18.00000000 -16.05555556 -14.22222222 -12.50000000
#> [306] -10.88888889 -9.38888889 -8.00000000 -6.72222222 -5.55555556
#> [311] -4.50000000 -3.55555556 -2.72222222 -2.00000000 -1.38888889
#> [316] -0.88888889 -0.50000000 -0.22222222 -0.05555556 0.00000000
#> [321] -0.05555556 -0.22222222 -0.50000000 -0.88888889 -1.38888889
#> [326] -2.00000000 -2.72222222 -3.55555556 -4.50000000 -5.55555556
#> [331] -6.72222222 -8.00000000 -9.38888889 -10.88888889 -12.50000000
#> [336] -14.22222222 -16.05555556 -18.00000000 -20.05555556 -22.22222222
#> [341] -24.50000000 -26.88888889 -29.38888889 -32.00000000 -34.72222222
#> [346] -37.55555556 -40.50000000 -43.55555556 -46.72222222 -50.00000000
#> [351] -53.38888889 -56.88888889 -60.50000000 -64.22222222 -68.05555556
#> [356] -72.00000000 -76.05555556 -80.22222222 -84.50000000 -88.88888889
#> [361] -93.38888889 -98.00000000 -102.72222222 -107.55555556 -112.50000000
#> [366] -117.55555556 -122.72222222 -128.00000000 -133.38888889 -138.88888889
#> [371] -144.50000000 -150.22222222 -156.05555556 -162.00000000 -168.05555556
#> [376] -174.22222222 -180.50000000 -186.88888889 -193.38888889 -200.00000000
#> [381] -206.72222222 -213.55555556 -220.50000000 -227.55555556 -234.72222222
#> [386] -242.00000000 -249.38888889 -256.88888889 -264.50000000 -272.22222222
#> [391] -280.05555556 -288.00000000 -296.05555556 -304.22222222 -312.50000000
#> [396] -320.88888889 -329.38888889 -338.00000000 -346.72222222 -355.55555556
#> [1] -48.02000000 -46.08000000 -44.18000000 -42.32000000 -40.50000000
#> [6] -38.72000000 -36.98000000 -35.28000000 -33.62000000 -32.00000000
#> [11] -30.42000000 -28.88000000 -27.38000000 -25.92000000 -24.50000000
#> [16] -23.12000000 -21.78000000 -20.48000000 -19.22000000 -18.00000000
#> [21] -16.82000000 -15.68000000 -14.58000000 -13.52000000 -12.50000000
#> [26] -11.52000000 -10.58000000 -9.68000000 -8.82000000 -8.00000000
#> [31] -7.22000000 -6.48000000 -5.78000000 -5.12000000 -4.50000000
#> [36] -3.92000000 -3.38000000 -2.88000000 -2.42000000 -2.00000000
#> [41] -1.62000000 -1.28000000 -0.98000000 -0.72000000 -0.50000000
#> [46] -0.32000000 -0.18000000 -0.08000000 -0.02000000 0.00000000
#> [51] -0.02000000 -0.08000000 -0.18000000 -0.32000000 -0.50000000
#> [56] -0.72000000 -0.98000000 -1.28000000 -1.62000000 -2.00000000
#> [61] -2.42000000 -2.88000000 -3.38000000 -3.92000000 -4.50000000
#> [66] -5.12000000 -5.78000000 -6.48000000 -7.22000000 -8.00000000
#> [71] -8.82000000 -9.68000000 -10.58000000 -11.52000000 -12.50000000
#> [76] -13.52000000 -14.58000000 -15.68000000 -16.82000000 -18.00000000
#> [81] -19.22000000 -20.48000000 -21.78000000 -23.12000000 -24.50000000
#> [86] -25.92000000 -27.38000000 -28.88000000 -30.42000000 -32.00000000
#> [91] -33.62000000 -35.28000000 -36.98000000 -38.72000000 -40.50000000
#> [96] -42.32000000 -44.18000000 -46.08000000 -48.02000000 -50.00000000
#> [101] -52.02000000 -54.08000000 -56.18000000 -58.32000000 -60.50000000
#> [106] -62.72000000 -64.98000000 -67.28000000 -69.62000000 -72.00000000
#> [111] -74.42000000 -76.88000000 -79.38000000 -81.92000000 -84.50000000
#> [116] -87.12000000 -89.78000000 -92.48000000 -95.22000000 -98.00000000
#> [121] -100.82000000 -103.68000000 -106.58000000 -109.52000000 -112.50000000
#> [126] -115.52000000 -118.58000000 -121.68000000 -124.82000000 -128.00000000
#> [131] -131.22000000 -134.48000000 -137.78000000 -141.12000000 -144.50000000
#> [136] -147.92000000 -151.38000000 -154.88000000 -158.42000000 -162.00000000
#> [141] -165.62000000 -169.28000000 -172.98000000 -176.72000000 -180.50000000
#> [146] -184.32000000 -188.18000000 -192.08000000 -196.02000000 -200.00000000
#> [151] -204.02000000 -208.08000000 -212.18000000 -216.32000000 -220.50000000
#> [156] -224.72000000 -228.98000000 -233.28000000 -237.62000000 -242.00000000
#> [161] -246.42000000 -250.88000000 -255.38000000 -259.92000000 -264.50000000
#> [166] -269.12000000 -273.78000000 -278.48000000 -283.22000000 -288.00000000
#> [171] -292.82000000 -297.68000000 -302.58000000 -307.52000000 -312.50000000
#> [176] -317.52000000 -322.58000000 -327.68000000 -332.82000000 -338.00000000
#> [181] -343.22000000 -348.48000000 -353.78000000 -359.12000000 -364.50000000
#> [186] -369.92000000 -375.38000000 -380.88000000 -386.42000000 -392.00000000
#> [191] -397.62000000 -403.28000000 -408.98000000 -414.72000000 -420.50000000
#> [196] -426.32000000 -432.18000000 -438.08000000 -444.02000000 -450.00000000
#> [201] -786.72222222 -773.55555556 -760.50000000 -747.55555556 -734.72222222
#> [206] -722.00000000 -709.38888889 -696.88888889 -684.50000000 -672.22222222
#> [211] -660.05555556 -648.00000000 -636.05555556 -624.22222222 -612.50000000
#> [216] -600.88888889 -589.38888889 -578.00000000 -566.72222222 -555.55555556
#> [221] -544.50000000 -533.55555556 -522.72222222 -512.00000000 -501.38888889
#> [226] -490.88888889 -480.50000000 -470.22222222 -460.05555556 -450.00000000
#> [231] -440.05555556 -430.22222222 -420.50000000 -410.88888889 -401.38888889
#> [236] -392.00000000 -382.72222222 -373.55555556 -364.50000000 -355.55555556
#> [241] -346.72222222 -338.00000000 -329.38888889 -320.88888889 -312.50000000
#> [246] -304.22222222 -296.05555556 -288.00000000 -280.05555556 -272.22222222
#> [251] -264.50000000 -256.88888889 -249.38888889 -242.00000000 -234.72222222
#> [256] -227.55555556 -220.50000000 -213.55555556 -206.72222222 -200.00000000
#> [261] -193.38888889 -186.88888889 -180.50000000 -174.22222222 -168.05555556
#> [266] -162.00000000 -156.05555556 -150.22222222 -144.50000000 -138.88888889
#> [271] -133.38888889 -128.00000000 -122.72222222 -117.55555556 -112.50000000
#> [276] -107.55555556 -102.72222222 -98.00000000 -93.38888889 -88.88888889
#> [281] -84.50000000 -80.22222222 -76.05555556 -72.00000000 -68.05555556
#> [286] -64.22222222 -60.50000000 -56.88888889 -53.38888889 -50.00000000
#> [291] -46.72222222 -43.55555556 -40.50000000 -37.55555556 -34.72222222
#> [296] -32.00000000 -29.38888889 -26.88888889 -24.50000000 -22.22222222
#> [301] -20.05555556 -18.00000000 -16.05555556 -14.22222222 -12.50000000
#> [306] -10.88888889 -9.38888889 -8.00000000 -6.72222222 -5.55555556
#> [311] -4.50000000 -3.55555556 -2.72222222 -2.00000000 -1.38888889
#> [316] -0.88888889 -0.50000000 -0.22222222 -0.05555556 0.00000000
#> [321] -0.05555556 -0.22222222 -0.50000000 -0.88888889 -1.38888889
#> [326] -2.00000000 -2.72222222 -3.55555556 -4.50000000 -5.55555556
#> [331] -6.72222222 -8.00000000 -9.38888889 -10.88888889 -12.50000000
#> [336] -14.22222222 -16.05555556 -18.00000000 -20.05555556 -22.22222222
#> [341] -24.50000000 -26.88888889 -29.38888889 -32.00000000 -34.72222222
#> [346] -37.55555556 -40.50000000 -43.55555556 -46.72222222 -50.00000000
#> [351] -53.38888889 -56.88888889 -60.50000000 -64.22222222 -68.05555556
#> [356] -72.00000000 -76.05555556 -80.22222222 -84.50000000 -88.88888889
#> [361] -93.38888889 -98.00000000 -102.72222222 -107.55555556 -112.50000000
#> [366] -117.55555556 -122.72222222 -128.00000000 -133.38888889 -138.88888889
#> [371] -144.50000000 -150.22222222 -156.05555556 -162.00000000 -168.05555556
#> [376] -174.22222222 -180.50000000 -186.88888889 -193.38888889 -200.00000000
#> [381] -206.72222222 -213.55555556 -220.50000000 -227.55555556 -234.72222222
#> [386] -242.00000000 -249.38888889 -256.88888889 -264.50000000 -272.22222222
#> [391] -280.05555556 -288.00000000 -296.05555556 -304.22222222 -312.50000000
#> [396] -320.88888889 -329.38888889 -338.00000000 -346.72222222 -355.55555556